数据结构第三天
本文共 3835 字,大约阅读时间需要 12 分钟。
链表
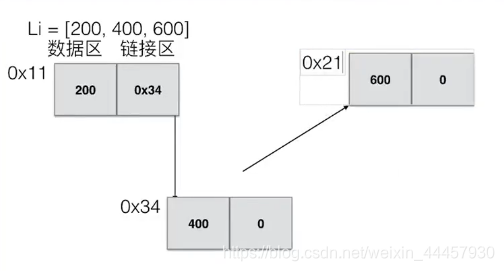
1 数据区与链接区
在以前学数据结构的时候,链表节点可以分成数据域和指针域,而python中,没有指针,只有引用,所以可以把链表节点分成数据区和链接区。
2 python中变量赋值的本质。
下面的复制语句,底层实现是什么?
a = 10 b = 20 变量a和b都是内存空间的名字,但a和b并不存放具体的数,而是存放对象的地址。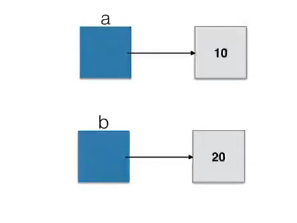 python中的赋值号不是赋值,而是引用,也就是说,传输的是地址。python中交换变量a,b的值,使用下面的表达式 a, b = b, a 赋值号右边相当于通过变量来访问对象的值,即20和10,而整个表达式相当于 a, b = 20, 10 即用元组赋值的方式,分别把20和10的地址赋给a和b
python中的赋值号不是赋值,而是引用,也就是说,传输的是地址。python中交换变量a,b的值,使用下面的表达式 a, b = b, a 赋值号右边相当于通过变量来访问对象的值,即20和10,而整个表达式相当于 a, b = 20, 10 即用元组赋值的方式,分别把20和10的地址赋给a和b 3 python语言实现单链表
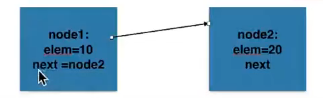
和C语言一样,需要先编写链表的结构体定义,这里将节点当成一个类(节点类):
class Node(object): """节点""" def __init__(self, elem): self.elem = elem self.next = None
is_empty() 链表是否为空 length() 链表长度 travel() 遍历整个链表 add(item) 链表头部添加元素 append(item) 链表尾部添加元素 insert(pos, item) 指定位置添加元素 remove(item) 删除节点 search(item) 查找节点是否存在
由于python是面向对象的语言,因此可以将链表当成一个类,将操作方法当成该类的成员函数。
链表一般都有表头节点,通常不存储数据,作用是使非空链表与空链表的操作统一。 相关代码如下:class SingleLinkList(object): """单链表""" def __init__(self, node=None): self.__head = node # 表头节点 def is_empty(self): """链表是否为空""" return self.__head == None def length(self): """链表长度""" # cur是current的缩写,指向当前位置,即为游标 cur = self.__head # count记录数量 count = 0 while cur != None: count += 1 cur = cur.next return count def travel(self): """遍历整个链表""" cur = self.__head while cur != None: print(cur.elem, end=" ") cur = cur.next print("") # 打印空字符串,表示换行 def add(self, item): """链表头部添加元素,头插法""" node = Node(item) node.next = self.__head self.__head = node def append(self, item): """链表尾部添加元素, 尾插法""" node = Node(item) if self.is_empty(): self.__head = node else: cur = self.__head while cur.next != None: cur = cur.next cur.next = node def insert(self, pos, item): """指定位置添加元素 :param pos 从0开始 """ if pos <= 0: self.add(item) elif pos > (self.length()-1): self.append(item) else: pre = self.__head count = 0 while count < (pos-1): count += 1 pre = pre.next # 当循环退出后,pre指向pos-1位置 node = Node(item) node.next = pre.next pre.next = node def remove(self, item): """删除节点""" cur = self.__head pre = None while cur != None: if cur.elem == item: # 先判断此结点是否是头节点 # 头节点 if cur == self.__head: self.__head = cur.next else: pre.next = cur.next break else: pre = cur cur = cur.next def search(self, item): """查找节点是否存在""" cur = self.__head while cur != None: if cur.elem == item: return True else: cur = cur.next return False 对上面的测试代码如下:
if __name__ == "__main__": ll = SingleLinkList() print(ll.is_empty()) print(ll.length()) ll.append(1) print(ll.is_empty()) print(ll.length()) ll.append(2) ll.add(8) ll.append(3) ll.append(4) ll.append(5) ll.append(6) # 8 1 2 3 4 5 6 ll.insert(-1, 9) # 9 8 1 23456 ll.travel() ll.insert(3, 100) # 9 8 1 100 2 3456 ll.travel() ll.insert(10, 200) # 9 8 1 100 23456 200 ll.travel() ll.remove(100) ll.travel() ll.remove(9) ll.travel() ll.remove(200) ll.travel()
链表操作注意事项:
1 单链表的操作,首先是考虑一般情况,然后考虑两种极限情况,即考虑在表头和表尾进行操作的情况,最后再考虑链表为空或者只有一个节点的情况。 2 插入的时候,先尽量不去动原有的指向关系。 3 链表操作,关键要确定建立哪些链接,打断哪些链接。4 其他链表
除了单链表外,还有单循环链表、双向链表、双循环链表等。
单循环链表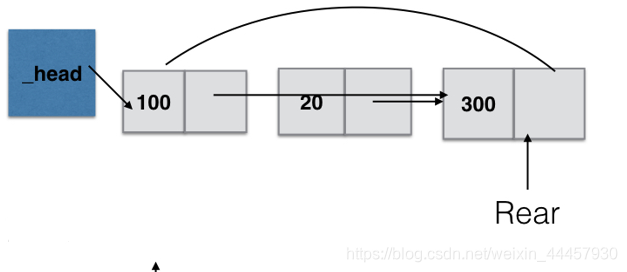 双向链表
双向链表 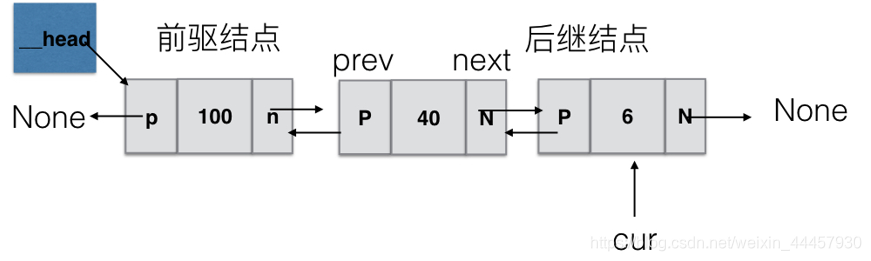 这些链表的操作类似于单链表。
这些链表的操作类似于单链表。 5 链表总结
无论各种链表,都有头结点,要记住各种链表的示意图,操作方法的具体代码不需要去记,但要知道过程,也就是能绘制出操作过程的示意图。
链表操作需要考虑三种边界情况: 1 表头和表尾进行操作的情况; 2 链表为空; 2 链表只有一个节点。转载地址:http://pkto.baihongyu.com/
你可能感兴趣的文章
NFS
查看>>
NFS Server及Client配置与挂载详解
查看>>
NFS 服务配置篇
查看>>
NFS共享文件系统搭建
查看>>
nfs复习
查看>>
NFS安装配置
查看>>
NFS服务器配置-服务启动与停止
查看>>
NFS的安装以及windows/linux挂载linux网络文件系统NFS
查看>>
NFS的常用挂载参数
查看>>
NFS网络文件系统
查看>>
NFS远程目录挂载
查看>>
nft文件传输_利用remoting实现文件传输-.NET教程,远程及网络应用
查看>>
NFV商用可行新华三vBRAS方案实践验证
查看>>
ng build --aot --prod生成文件报错
查看>>
ng 指令的自定义、使用
查看>>
ng6.1 新特性:滚回到之前的位置
查看>>
nghttp3使用指南
查看>>
Nginx
查看>>
nginx + etcd 动态负载均衡实践(一)—— 组件介绍
查看>>
nginx + etcd 动态负载均衡实践(三)—— 基于nginx-upsync-module实现
查看>>